SINGLE PAYMENT FORMULAE

 

If we invest a Present Sum P for n interest periods at an interest rate i per interest period, this will yield a Final Sum S at the end of n periods.

The following diagrammatic illustration will facilitate your understanding of the inter-relationship between the Single Payment Formulae parameters.

Single Payment/Investment (P)
at Time Zero

 

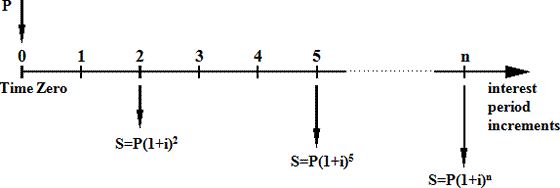
If we invest P for 1 interest period at the interest rate i per interest period, then

S at the end of 1 interest period=P + Pi=P( 1 + i )

If we invest P for 2 interest periods at the interest rate i per interest period, then

S at the end of 2 interest period=P( 1 + i ) ( 1 + i )=P( 1 + i )2

If we invest P for 3 interest periods at the interest rate i per interest period, then

S at the end of 3 interest period=P( 1 + i ) ( 1 + i ) (1 + i )=P( 1 + i )3

If we invest P for n interest periods at the interest rate i per interest period, then

S at the end of n interest periods=P( 1 + i )n

Hence the following formulae :-

(F1)S=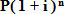

(F2)P=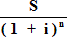

If we borrow the sum P over n interest periods at interest rate i per interest period, then we will be required to repay the sum S at the end of the n periods.

---

 

Illustration of Logarithmic Solution using Example 5.2    
                  

If we invest a Present Sum (P) of £10,000 for a period of 5 years and we will receive a Final Sum (S) of £17,860.71 at the end of the 5 year period, what (Internal) Rate of Return (i) will we have earned on our investment?

From Formula (F1) we have: S=P( 1 + i )ⁿ

=( 1 + i )ⁿ        

Note!  If you have a scientific calculator with a 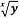  function on it, you could work out the value of  i  immediately, at this stage.

       =         =    12.3%p.a. 

                          

The value of i is computed using Logarithms as follows:

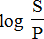=log ( 1 + i )ⁿ=n log ( 1 + i )

 

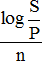=log ( 1 + i )

log ( 1 + i )       =         0.0504

    ( 1 + i )         =         10^0.0504

Giving:    i         =         10^0.0504   - 1=12.3%p.a.