Let us now compare the APR in the three Mortgage Illustrations outlined above. For clarity of understanding refer back to each Illustration in turn. (See Section 6.2.)

Illustration 1: APR Computation

First National Building Society (May 1991)

Amount Borrowed£35,000 over 20 Years.
Mortgage Interest Rate Quoted11.85% p.a.
Monthly Repayment Charge£386.81.

The Amount Borrowed is to be repaid by 240 End of Month Monthly Repayments of £386.81

Therefore:R=£386.81

P=£35,000

n=240 months

i=?

We want to compute the interest rate being charged over the time period increment, which in this case is one month.

Using Formula (F5)R=P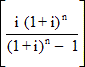

i.e.£386.81=£35,000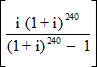

We want to compute the value of i that satisfies this expression.

By iteration, i computes at 1.005% per month.

The Monthly % Rate of charge is therefore 1.005%.

The Annual Percentage Rate (APR) of charge is computed by compounding the monthly % Rate of charge to 12 months.

i.e.APR=100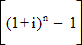

Note! The expression 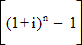gives the Annual Rate of Charge in terms of a decimal fraction; we then multiply this decimal fraction by 100 to convert to percentage.

                         i=1.005% per month

n=12 months

Giving:APR=100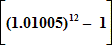

=12.749%

Illustration 2: APR Computation

Some Competitor Financial Institution. (Illustration Example)

Amount Borrowed£35,000 over 20 Years.
Mortgage Interest Rate Quoted12.06% p.a.
Monthly Repayment Charge£386.85.

Monthly Interest Rate Charged = 1.005%,i.e.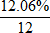

Giving:APR=12.749% (as already computed above)

Illustration 3: APR Computation

Some Competitor Financial Institution. (Illustration Example)

Amount Borrowed£35,000 over 20 Years.
Mortgage Interest Rate Quoted11.85% p.a.
Monthly Repayment Charge£381.73.

Monthly Interest Rate Charged = 0.9875%,i.e.

Giving:APR=100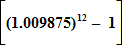

=12.515%

                                                    -----------------



Comparing the above Illustrations:

                                                    -----------------


From the above Illustrations it is clear that a statement of Annual Percentage Rate (APR) of charge provides the borrower with a statute defined yardstick that enables him to make a true comparison of the ‘cost of credit’ as charged by the various Lending Institutions.

It is also clear that the failure by First National / Irish Life to indicate the APR on their Mortgage Quotation would be likely to mislead a borrower; it would also be likely to afford First National / Irish Life an unfair advantage over a competitor Financial Institution.