7.1 The Expected Return on Investment
You will note in the presentation of the Mortgage Quotations for Case 1 and Case 2 (see Appendix 1/2) where we are told that, with the Endowment Mortgage, the Surplus and Early Repayment Term are calculated 'assuming a unit growth rate of 10.75 % p.a. less a management charge of 1/12 % per month'.
We are also told that this assumed growth rate is not a forecast and the amount payable may be greater or less than illustrated.
Is the assumed growth rate a rate that can be reasonably expected to be achieved ?
— We don’t know !
— We are not told !
What are the chances that the assumed growth rate will be achieved ?
— We don’t know !
— We are not told !
What are the chances that the growth rate achieved will be greater than the assumed growth rate ?
— We don’t know !
— We are not told !
What are the chances that the growth rate achieved will be less than the assumed growth rate ?
— We don’t know !
— We are not told !
What is the measure of the RISK associated with choosing the Endowment Mortgage rather than the Repayment Mortgage ?
— We don’t know !
— We are not told !
Based on the assumed growth rate being achieved, what is the excess Rate of Return achieved by choosing the Endowment Mortgage that justifies accepting the RISK associated with the Endowment Mortgage, rather than opting for the Repayment Mortgage ?
— We don’t know !
— We are not told !
No information whatsoever is given regarding the RISK associated with the Endowment Mortgage ─── in fact, the concept of RISK is not even mentioned. It is vitally important, before we proceed further with Case analyses, that we have a clear understanding of the concept of RISK.
We will illustrate the concept of RISK by using a number of Examples.
Example 7.1
Consider an investment in Investment Portfolio Option A, where the yearly Returns achieved by investing in this Investment Portfolio Option over the past 20 years is known, and is as shown on the following tabulation.
|
Year. |
Return (% p.a.) |
|
1 |
10 |
|
2 |
4 |
|
3 |
26 |
|
4 |
2 |
|
5 |
12 |
|
6 |
4 |
|
7 |
10 |
|
8 |
2 |
|
9 |
6 |
|
10 |
30 |
|
11 |
10 |
|
12 |
12 |
|
13 |
26 |
|
14 |
6 |
|
15 |
4 |
|
16 |
2 |
|
17 |
10 |
|
18 |
6 |
|
19 |
4 |
|
20 |
12 |
If we are to invest in Investment Portfolio Option A, and our investment decision is to be based on an objective assessment of this Portfolio Option’s historical return data for the past 20 years, what Return can we Expect on our investment?
The Expected Return is the average return achieved over the 20 year period and is therefore calculated by adding up the Returns achieved each year and dividing the total by 20.
Expected Return =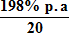 
= 9.9% p.a.
---------------
You will note from the above tabulation that some Return values were achieved more frequently than others. By tabulating the frequency with which each Return value achieved is distributed over the 20 year period, we put the return data into a format that facilitates its Statistical Analysis, thus providing the fundamental financial parameters necessary for an informed investment decision.
---------------
The frequency of the yearly Returns on investments in the Investment Portfolio Option A described above is as shown on the following Distribution Table. (This is called the portfolio’s Return / Frequency Distribution.)
|
Return
(x % p.a.)
|
Number of years this Return of x % p.a. has been achieved over the 20 year period. (Frequency) |
Probability of achieving this return of x % p.a. in any one year (Probability Distribution) |
|
2% |
3 |
3/20 = 0.15 |
|
4% |
4 |
4/20 = 0.2 |
|
6% |
3 |
3/20 = 0.15 |
|
10% |
4 |
4/20 = 0.2 |
|
12% |
3 |
3/20 = 0.15 |
|
26% |
2 |
2/20 = 0.1 |
|
30% |
1 |
1/20 = 0.05 |
From the above Frequency Distribution Table we can deduce the Probability Distribution Table (shown alongside it) as follows:
| (a) |
there is a 3 in 20 chance that our return will be 2 % p.a. |
| (b) |
there is a 4 in 20 chance that our return will be 4 % p.a. |
| (c) |
there is a 3 in 20 chance that our return will be 6 % p.a. |
| (d) |
there is a 4 in 20 chance that our return will be 10 % p.a. |
| (e) |
there is a 3 in 20 chance that our return will be 12 % p.a. |
| (f) |
there is a 2 in 20 chance that our return will be 26 % p.a. |
| (g) |
there is a 1 in 20 chance that our return will be 30 % p.a. |
The Expected Return is computed by weighting each Return value by the Frequency of that Return and dividing by the total number of years (in this case 20 years).
The Expected Return on our investment is, therefore, the Weighted Average Return.
| Expected Return | = |
(2% x 3) + (4% x 4) + (6% x 3) + (10% x 4) + (12% x 3) + (26% x 2) + (30% x 1) 20 |
| = | 9.9 % p.a. |
---------------
The Expected Return can also be computed by weighting each Return value by the Probability of that Return value being achieved.
Note! In ‘Statistics’ terms, the Expected Return is the mean of the investment portfolio’s Return / Probability Distribution.
| Expected Return | = |
(2% x 0.15) + (4% x 0.2) + (6% + 0.15) + (10% x 0.2)
+ (12% x 0.15) + (26% x 0.1) + (30% x 0.05) |
| = | 9.9% p.a. |
The general Statistics formula for the Expected Value of the Return (i.e. the Expected Return) can be extrapolated from the above (Example 7.1).
| Expected Return | = |
The Sum of ‘the products of each Return value multiplied by the Probability of that Return value being achieved’.
|
If there are n Return values, each with a separate value xi and a corresponding Probability of Occurrence PRi for i = 1 to n , then the Expected Return E(x) on our investment is:
| (F9) | E(x) | = |
n Σi = 1 |
PRi Xi |
| Note! | The Symbol | Σ | denotes ‘ The Sum of ’ |
| The Symbol |
n Σi = 1 |
denotes ‘ The Sum of : from i = 1 to n ’ |
Using the parameters of Example 7.1 above:
n = 7 , i.e. there are 7 Return Values.
For i = 1 to 7 we have :
|
x1
|
=
|
2 % with PR1
|
=
|
0.15
|
x2 |
= |
4 % with PR2 |
= |
0.2 |
x3 |
= |
6 % with PR3 |
= |
0.15 |
x4 |
= |
10 % with PR4 |
= |
0.2 |
x5 |
= |
12 % with PR5 |
= |
0.15 |
x6 |
= |
26 % with PR6 |
= |
0.1 |
x7 |
= |
30 % with PR7 |
= |
0.05 |
So our Expected Return E(x) is given by:
| E(x) | = | (0.15 x 2%) + (0.2 x 4%) + (0.15 x 6%) + (0.2 x 10%) + (0.15 x 12%) + (0.1 x 26%) + (0.05 x 30%) |
| = | 9.9% p.a. as above |