Appendix 5/2
Derivation of Uniform Series Payment Formulae
UNIFORM SERIES PAYMENT FORMULAE
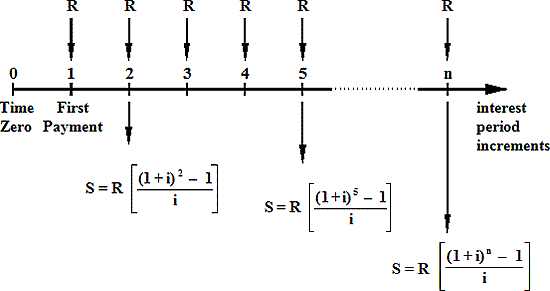
If we invest an equal amount R at the end of each period for a duration of n periods at an interest rate i per interest period, these investments will yield a Final Sum S at the end of the n periods.
The following diagrammatic illustration will facilitate your understanding of the inter-relationship between these Uniform Series Payment Formulae parameters.
Uniform (i.e. equal in amount) Series of Payments (R)
i = interest rate per
interest period
|
Interest |
Sum at start of |
Sum at End of Interest Periods, S |
|
1 |
Nil |
R |
|
2 |
R |
R(1 + i ) + R |
|
3 |
R(1 + i ) + R |
R(1 + i )2 + R(1 + i ) + R |
|
4 |
R(1 + i )2 + R(1 + i ) + R |
R(1 + i )3 + R(1 + i )2 + R(1 + i ) + R |
|
5 |
R(1 + i )3 + R(1 + i )2 + R(1 + i ) + R |
R(1 + i )4 + R(1 + i )3 + R(1 + i )2 + R(1 + i ) + R |
|
n |
R(1 + i )n-2 + R(1 + i )n-3 +......+ R(1 + i ) + R |
R(1 + i )n-1 + R(1 + i )n-2 +........... + R(1 + i ) + R |
It can also be seen from the development of the expressions for the 'Sum at the End of Interest Periods, S, that our Uniform Series Payment Formulae could be derived using Mathematical Induction.
Here, we will develop the formulae from the Geometric Series.
The general form for a Geometric Series is:
Sn = [a + ar + ar2 + ar3 + .......... + arn-2 + arn-1]
For the general Geometric Series formula:
Sn = a + ar + ar2 + ar3 + ar4+ .......... + arn-2 + arn-1
rSn = ar + ar2 + ar3 + ar4 + ar5+ .......... + arn-1 + arn
Sn - rSn = a - arn
Sn (1 - r ) = a (1 - rn )
Sn = ![]()
In the current situation: Sn = R(1 + i )n-1 + R(1 + i )n-2 +........... + R(1 + i ) + R
i.e. Sn = R[(1 + i )n-1 + (1 + i )n-2 +........... + (1 + i ) + 1]
We can therefore apply the mathematical proofs from the general Geometric Series formula to our current situation.
The current situation can therefore be assessed as follows:
Sn = R![]()
In this Geometric Series: a = (1 + i )n-1 and ![]()
Substituting for a and r in the Geometric Series formula yields:
Sn = R 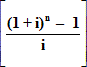
Formula (F3)S=R 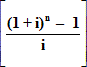
Formula (F4)R=S 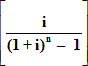
But from Formula (F1) (see Appendix 5/1) we know that the Final Sum S at the end of n interest periods can also be realised by investing a Present Sum P at interest rate i per interest period over the n periods.
i.e. S=P ( 1 + i )n
Substituting this expression for S in Formula (F4) gives :
R=P (1 + i)n 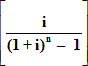
Hence the following formulae:-
Formula (F5)R=P 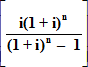
Formula (F6)P=R 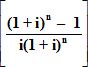
So if we invest a Present Sum P for n interest periods at interest rate i per interest period this would mature to a Final Sum S at the end of n periods.
i.e.S = P( 1 + i )n
However instead of allowing our investment to mature to the Final Sum S at the end of the n periods we may withdraw equal amounts R at the end of each period over the n periods.
i.e. R=P 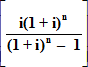
When you borrow money the lending institution is effectively investing a sum of money in you, the borrower. Therefore if we borrow a Present Sum P, as in an Annuity (Repayment) Mortgage, over n interest periods at an interest rate i per interest period, we repay the loan by repaying equal amounts R at the end of each of the interest periods.
Therefore formula (F5) is the formula used for computing repayments on an Annuity / Repayment Mortgage.
Illustration of Logarithmic Solution using Example 5.3
If we borrow a Present Sum (P) of £7,581.57 at an interest rate of 10% p.a. and we repay this loan by repaying £2,000 (R) at the end of each year, then at the end of what time period will our loan be fully repaid?
R=P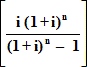
£2,000 = £7,581.57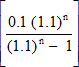
0.2637976 = 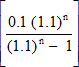
2.637976 [(1.1)n - 1] = (1.1)n
2.637976 (1.1)n - 2.637976 = (1.1)n
(1.1)n (2.637976 - 1.1) = 2.637976
(1.1)n = 1.610509556
n log (1.1) = log (1.610509556)
n = 5 years