Appendix 5/1
Derivation of Single Payment Formulae
Note! The formulae derivations of Appendix 5/1 and Appendix 5/2 are included for ‘first principles’ purists like myself, and to pre-empt any credulity being given to the customary denial position adopted by the Financial Services Institutions.
SINGLE PAYMENT FORMULAE
If we invest a Present Sum P for n interest periods at an interest rate i per interest period, this will yield a Final Sum S at the end of n periods.
The following diagrammatic illustration will facilitate your understanding of the inter-relationship between the Single Payment Formulae parameters.
Single Payment/Investment (P)
at Time Zero
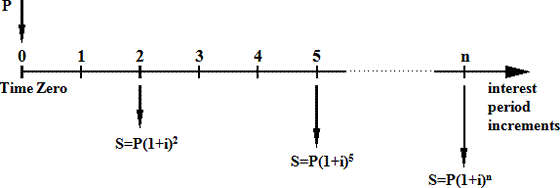
If we invest P for 1 interest period at the interest rate i per interest period, then
S at the end of 1 interest period=P + Pi=P( 1 + i )
If we invest P for 2 interest periods at the interest rate i per interest period, then
S at the end of 2 interest period=P( 1 + i ) ( 1 + i )=P( 1 + i )2
If we invest P for 3 interest periods at the interest rate i per interest period, then
S at the end of 3 interest period=P( 1 + i ) ( 1 + i ) (1 + i )=P( 1 + i )3
If we invest P for n interest periods at the interest rate i per interest period, then
S at the end of n interest periods=P( 1 + i )n
Hence the following formulae :-
(F1)S=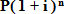
(F2)P=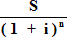
If we borrow the sum P over n interest periods at interest rate i per interest period, then we will be required to repay the sum S at the end of the n periods.
Illustration of Logarithmic Solution using Example 5.2
If we invest a Present Sum (P) of £10,000 for a period of 5 years and we will receive a Final Sum (S) of £17,860.71 at the end of the 5 year period, what (Internal) Rate of Return (i) will we have earned on our investment?
From Formula (F1) we have: S=P( 1 + i )n
![]() =( 1 + i )n
=( 1 + i )n
Note! If you have a scientific calculator with a 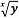 function on it, you could work out the value of i immediately, at this stage.
function on it, you could work out the value of i immediately, at this stage.
![]() =
= ![]() = 12.3%p.a.
= 12.3%p.a.
The value of i is computed using Logarithms as follows:
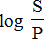 =log ( 1 + i )n=n log ( 1 + i )
=log ( 1 + i )n=n log ( 1 + i )
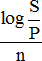 =log ( 1 + i )
=log ( 1 + i )
log ( 1 + i ) = 0.0504
( 1 + i ) = 100.0504
Giving: i = 100.0504 - 1=12.3%p.a.
