While an indication of the APR effectively discloses the true ‘cost of credit’ being charged by the various Financial Institutions, it does not disclose (where such is the case) the FACT that interest is being compounded on an annual basis. Nor does it disclose the FACT that the manner in which Financial Institutions charge annually compounded interest may result in further penal consequences for the borrower. These are material facts.


If the borrower, as is often the case, chooses to pay off a lump sum against the Principal Outstanding on his Mortgage Loan, such a lump sum payment may be of much less benefit to him in the case where interest is compounded on an annual basis than in the case where interest is compounded on a monthly basis.


Where Financial Institutions compound their interest charged on an annual basis, they generally engage in a practice whereby the monthly interest they charge for each month throughout the year is calculated on the full Amount Outstanding on the Borrower’s Loan Account at the beginning of the year (i.e. on the Opening Balance). A comparison of the following Illustrations will clearly show how this surreptitious practice can have a seriously negative impact on the borrower’s financial position.


Note! Throughout the following Illustrations we have assumed that the interest rate applicable does not change; this is to ensure clarity of the substantive issue raised.

Illustration 4

Consider first the situation where a couple, Couple A, with 20 years left to run on their Mortgage Term, have an Amount Outstanding on their Loan Account at the start of the year (i.e. the beginning of January) of £35,000. The interest rate charged by their Financial Institution is 11.85% p.a., and Monthly Repayments are computed by them on the basis of compounding the interest charge annually in the manner as described in Illustration 1 of Section 6.2. Their Financial Institution calculates its interest due charge for the year, and consequently for each month throughout the year, on the basis of the Amount Outstanding on the borrower’s Loan Account at the beginning of the year.


The Loan Account parameters for Couple A will therefore be similar to those applicable in Illustration 1 of Section 6.2, and will be as follows:

Amount Outstanding£35,000
Mortgage Interest Rate11.85% p.a.
Remainder of Mortgage Term20 years
Monthly Repayment£386.81

The Balancing Statement of the Loan Account for Couple A at the end of the year (i.e. Balancing Statement 1) would be as follows:

Note! Because interest is compounded on an annual basis, this means that the monthly repayments are calculated by dividing the Annuity Payment by 12. The Interest Due element of this monthly repayment is in turn calculated by dividing the annually compounded Interest Due by 12 (i.e. £35,000 x 11.85% = £4147.50 annual Interest; £4147.50 divided by 12 = £345.62).

So, Couple A, on the following January 1st, with 19 years left to run on their Mortgage Term, would have an Amount Outstanding on their Loan Account of £34,505.72.

But what if Couple A paid off a lump sum of £10,000 against their Mortgage Loan during the previous year ?

What would be the net effect of this lump sum payment on their end of year Closing Balance ?

If Couple A had paid off a Lump Sum of £10,000 against their Mortgage Loan at the end of February, because their Financial Institution computed its monthly interest due charge for each month throughout the year on the basis of the Opening Balance on the borrower’s Loan Account at the start of the year, no benefit from a reduction of Interest Due would accrue to them until the start of the following year. This fact is clearly evident from the Balancing Statement at the end of the year (i.e. Balancing Statement 2) which, taking account of a lump sum payment of £10,000 in February, would read as follows:

Note! For clarity of illustration, we have assumed that Couple A have elected to continue with the same monthly repayments, notwithstanding the lump sum payment. (Most couples, as a matter of financial prudence, would adopt this course of action in any case.)

So, even if Couple A paid off a lump sum of £10,000 against their Mortgage Loan at the end of February, the net effect of this lump sum payment would be to reduce the Closing Balance on their Loan Account at the end of the year (i.e. 10 months later) by only £10,000. This is because no reduction in Interest Due charged by the Lending Institution resulted from the lump sum payment. This would only come into effect in January of the following year, as it would only reduce the Opening Balance at this stage.

The full extent of the negative effect that this furtive practice by such Financial Institutions can have on the borrower’s financial position is most clearly seen when one instances similar circumstances with a Financial Institution that compounds and charges, interest due, on a monthly basis. This we will now do.

Illustration 5

Consider now the situation where another couple, Couple B, with 20 years left to run on their Mortgage Term, have an Amount Outstanding on their Loan Account at the start of the year (i.e. the beginning of January) of £35,000. The interest rate charged by their Financial Institution is 11.85% p.a., and Monthly Repayments are computed by them by compounding interest on a monthly basis in the manner as described in Illustration 3 of Section 6.2.


The Loan Account parameters for Couple B will therefore be similar to those applicable in Illustration 3 of Section 6.2 and will be as follows:

Amount Outstanding£35,000
Mortgage Interest Rate11.85% p.a.
Remainder of Mortgage Term20 years
Monthly Repayment£381.73

Note! Because interest is compounded on a monthly basis, this means that the monthly repayments are in the form of a Uniform Monthly Series of payments. It also means that the Interest Due charged each month is 0.9875% (11.85% x 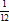) of the Principal Outstanding at the end of the previous month.

So, Couple B, on the following January 1st, with 19 years left to run on their Mortgage Term, would have an Amount Outstanding on their Loan Account of £34,542.41.

But what if Couple B had paid off a lump sum of £10,000 against their Mortgage Loan during the previous year ?

What would be the net effect of this lump sum payment on their end of year Closing Balance ?

If Couple B had paid off a Lump Sum of £10,000 against their Mortgage Loan at the end of February, because their Financial Institution computed its monthly interest due charge for each month by compounding the monthly interest rate on the Amount Outstanding on the borrower’s Loan Account at the beginning of that month (i.e. the end of the previous month), the full benefit from a reduction of Interest Due would accrue to them immediately (i.e. from the beginning of March).


The benefits accruing to Couple B are in stark contrast with the lack of same in the case of Couple A in the previous Illustration (Illustration 4). This fact is clearly evident from the Balancing Statement of Couple B at the end of the year (i.e. Balancing Statement 4) which, taking account of a lump sum payment of £10,000 at the end of February, would read as follows:

Note! Again, for clarity of illustration and ease of comparison, we have assumed that Couple B elected to continue with the same monthly repayments they were making prior to paying off the lump sum.

So, if Couple B paid off a lump sum of £10,000 against their Mortgage Loan at the end of February, the net effect of this lump sum payment would be to reduce the Closing Balance on their Loan Account at the end of the year (i.e. 10 months later) by £11,032.54, (£11,032.54 being the difference between the Closing Balances of Balancing Statement 3 and Balancing Statement 4).

                                               -------------------------

A comparison of the two previous Illustrations (in the cases where a £10,000 lump sum was paid off at the end of February) shows that, with 19 years left to run on their original Mortgage Term, Couple A are £1,032.54 worse off than Couple B.


Further insult is added to this financial injury inflicted on Couple A, in that they will suffer the additional burden of repaying this outstanding amount of £1,032.54 (together with interest charged) over the remainder of the Mortgage duration.

When expressed in Final Value terms, based on a Mortgage Interest Rate of 11.85% p.a. compounded monthly, £1032.54 has a Final Value of £9,703.41 at the end of the Mortgage Term, i.e. 19 years later.

When one compares this Final Value to any Projected Surplus After Loan Repaid (this too being an ‘end of mortgage term’ Value) pertaining to an Endowment Mortgage Policy, the significance of this additional burden that may be suffered by the borrower, where interest is compounded on an annual basis, becomes clearly evident.

For example, the Mortgage represented to me at my initial pre-contract meeting with the First National Building Society (see Case 1 of Appendix 1/2) was for £35,000 borrowed over 20 years @ 11.85% (exactly as in Illustration 4 above) and this representation touted a Projected Surplus After Loan Repaid of £12,770 at the end of the 20 year term. This shows the major significance of Final Value of £9,703.41 by which Couple A would be worse off where the interest was compounded annually. 

Note! The difference in the benefit to the borrower is obviously dependent on the time at which the lump sum payment is made. For example, if the lump sum payment against the Mortgages was paid at the end of December in the cases illustrated above the difference would be zero, as the reduction would take full and immediate effect on the Opening Balance for the following year. But the material significance of the potentially injurious effect on borrower's financial position, where interest is compounded on an annual basis, cannot be denied.


                                                       ---------------


While the comparison of situations for Couple A and Couple B above is contrived to illustrate the financially injurious effect, it is nonetheless patently clear that, where Financial Institutions who compound interest annually engage in the practice whereby the interest due they charge for each month throughout the year is computed on the basis of the Opening Balance on the borrower’s Loan Account at the start of each year, this potential to have a detrimental effect on the borrower’s financial position is very real indeed.

The fact that such Financial Institutions may engage in this practice furtively, without the knowledge of the borrower, means that the borrower will generally be unaware of the injury caused him.

He won’t feel a thing !