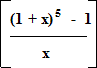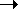5.3 The Basic Tools of Investment Analysis
We have seen from Example 5.4 that, for an annual cost of investment of £3,000 at the end of each year for a period of 5 years, a Final Value of £19,518.13 received at the end of the five year investment period means that we will have achieved an (Internal) Rate of Return of 13.2% p.a. on our investment.
The computation of the (Internal) Rate of Return required using an iterative ‘trial and error’ process.
Consider now the situation where our Annual Cost of £3,000 is subsidised by some outside incentive such as a government subsidy, gratuity or tax relief.
Example 5.5
Our Gross Annual Cost of investment in a Building Society is £3,000 per year at the end of each year for a period of 5 years. Our choice of this investment means that we will receive a government subsidy, to the value of 20% of our gross investment outlay, at the time of our investment (i.e. at the end of each of the 5 years). If the Building Society pays us an interest rate of 13.2% p.a. on our investment, what Internal Rate of Return have we achieved on our net outlays, and what was our Equivalent Annual Cost for this investment?
Note! Our ‘Net Outlay’ is what we actually ended up paying out, i.e. what the investment actually cost us; it is, therefore, our gross investment outlay less the government subsidy.
INTERNAL RATE OF RETURN
The Internal Rate of Return (IRR) is the interest return actually achieved on the Net Outlays.
EQUIVALENT ANNUAL COST
The Equivalent Annual Cost (EAC) is the equal amount end of each year Net Outlay (i.e. the Uniform Annual Series of Payments) that will realise exactly the same Final Value as the summation of the final values of each individual end of year Net Outlay, at an interest rate equal to the Internal Rate of Return.
Note ! The Equivalent Annual Cost, therefore, directly relates to the Internal Rate of Return (and vice versa).
Note! Your understanding of these Financial Analysis parameters, i.e. Internal Rate of Return (IRR) and Equivalent Annual Cost (EAC), will become much clearer from the Examples that follow.
In this Example, our investment in the Building Society is £3,000 at the end of each year for a period of 5 years. The Building Society gives us an interest rate of 13.2% p.a. on our investment. Therefore, the Final Value we will receive from the Building Society at the end of the 5 year investment period is computed using formula (F3).
(F3)S=R 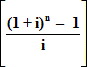
R = £3,000i = 13.2%n = 5 years
HenceS=£3,000 
giving the Final ValueS=£19,518.13
However, our Net Outlay was less than £3,000 at the end of each year because of the government subsidy received, and therefore our Internal Rate of Return (i.e. the return we have actually achieved on our Net Outlay costs) will be higher than the 13.2% p.a. paid by the Building Society.
For clarity, and for ease of comparison with future examples, we first compute the Net Outlay for each year by tabulating as follows:
|
End of |
Gross |
Government |
Net |
|
1 |
£3,000 |
£600 |
£2,400 |
|
2 |
£3,000 |
£600 |
£2,400 |
|
3 |
£3,000 |
£600 |
£2,400 |
|
4 |
£3,000 |
£600 |
£2,400 |
|
5 |
£3,000 |
£600 |
£2,400 |
Because we are dealing with equal amount Net Outlays at the end of each year (i.e. because our Net Outlays already constitute a uniform series of payments), our Equivalent Annual Cost is immediately apparent, being £2,400 per year. We can therefore use the Uniform Series Formula (F3), directly, in an iterative process (as we did in Example 5.4), to compute the Internal Rate of Return. This process is tabulated as follows:
Let the Internal Rate of Return (IRR)=x% p.a.
|
Trial |
End of year |
Trial |
Computed value |
Computed value S = £2,400 |
|
1 |
£2,400 |
20% |
7.4416 |
£17,859.84 |
|
2 |
£2,400 |
24% |
8.048438 |
£19,316.25 |
|
3 |
£2,400 |
24.5% |
8.127384 |
£19,505.72 |
|
4 |
£2,400 |
24.533% |
8.13261869 |
£19,518.28 O.K. |
So, the Internal Rate of Return (IRR) we have achieved on our investment is 24.533% p.a., with an Equivalent Annual Cost (EAC) of £2,400. Comparing this Example to Example 5.4, we can see that for a similar Gross Outlay of £3,000 at the end of each year, we have achieved a much higher Internal Rate of Return (24.533% compared to 13.2%) as a result of the annual government subsidy of £600.
In Example 5.5, the Net end of year Outlay was equal each year at £2,400 (i.e. our Net Outlays were ALREADY uniform) and we were therefore able to use a Uniform Series Formula, directly, in an iterative process, to compute the Internal Rate of Return. We will now consider the situation where the Net Annual Outlay differs each year, this being the situation with a Repayment Mortgage (where the amount of Tax Relief on Interest Paid reduces each year, or after a number of years).
Example 5.6
Our Gross Annual Cost of investment in a Building Society is £3,000 per year at the end of each year for a period of 5 years, and this choice of investment means that we will receive a government subsidy at the end of each of the five years. This government subsidy will vary linearly over the five years as follows:
ForYear 1Subsidy=40% of Gross Investment
ForYear 2Subsidy=30% of Gross Investment
ForYear 3Subsidy=20% of Gross Investment
ForYear 4Subsidy=10% of Gross Investment
ForYear 5Subsidy=0% of Gross Investment
If the investment interest rate paid by the Building Society on our investment is 13.2% p.a., our investment thereby yielding a Final Value of £19,518.13 from the Building Society, what Internal Rate of Return (IRR) have we achieved on our Net Outlays and what was our Equivalent Annual Cost (EAC) for this investment?
We first compute the Net Outlay for each year by tabulating as follows:
|
Year |
Gross Outlay |
Government |
Net Outlay |
|
1 |
£3,000 |
£1,200 |
£1,800 |
|
2 |
£3,000 |
£900 |
£2,100 |
|
3 |
£3,000 |
£600 |
£2,400 |
|
4 |
£3,000 |
£300 |
£2,700 |
|
5 |
£3,000 |
Zero |
£3,000 |
Because our Net Outlays are not the same for each year (i.e. because our Net Outlays are not uniform), they do not constitute a Uniform Series of payments, and our Equivalent Annual Cost (EAC) is not immediately apparent. We must therefore compute the Internal Rate of Return (IRR) before we can establish the Equivalent Annual Cost (EAC). This is done as follows.
Let the Internal Rate of Return (IRR)=x% p.a.
The Final Value (FV) of our investment IS EQUAL TO the Sum of the final values ( Σ fv) achieved by each year's Net Outlay invested at x% p.a. over the investment period applicable to that Net Outlay.
Formula (F7)FV=Σ fv
Note! The symbol Σ denotes ‘ The Sum of ’
Alternatively, the Present Value (PV) of our investment, this being the value of the Final Value (FV) at Time Zero (i.e. the Final Value discounted at the Internal Rate of Return of x% p.a. to Time Zero), IS EQUAL TO the Sum of the present values ( Σ pv) of each year's Net Outlay, the present values being the Time Zero values of each year’s Net Outlay discounted at the Internal Rate of Return of x% p.a.
Formula (F8)PV=Σ pv
Note! Formulae (F7) and (F8) are logically equivalent formulae. (This will be proved below.)
In this example, Example 5.6, our Final Value (FV) is £19,518.13. We want to compute the value of the Internal Rate of Return, x% p.a., such that : when each of our Net Outlays is invested at x% p.a. over the investment time period applicable to that Net Outlay, the Sum of their final values ( Σ fv) will be equal to our Final Value (FV) of £19,518.13.
FV=Σ fv
Remember! S=P(1 + i)n
The final value (fv) yielded by the end of the first year’s Net Outlay of £1800 is therefore fv = £1,800 (1+x)4, the Investment Time Period applicable being 4 Years.
Σ fv is calculated by tabulating the final value (fv) of each year’s Net Outlay and summating as follows:
|
Year |
Net Outlay |
Investment |
final value |
|
1 |
1,800 |
4 |
1,800 (1 + x)4 |
|
2 |
2,100 |
3 |
2,100 (1 + x)3 |
|
3 |
2,400 |
2 |
2,400 (1 + x)2 |
|
4 |
2,700 |
1 |
2,700 (1 + x)1 |
|
5 |
3,000 |
0 |
3,000 |
|
FV = Σ fv |
|||
Therefore FV = Σ fv = £1,800 (1 + x)4 + £2,100 (1 + x)3 + £2,400 (1 + x)2
+ £2,700 (1 + x) + £3,000 = £19,518.13
The value of the Internal Rate of Return, x% p.a., that makes this expression [i.e. the above equation for the Final Value (FV)] valid is computed using Iteration. This ‘trial and error’ process is most clearly done by tabulation, as follows:
|
Year |
Net Outlay (Year End) £ |
Investment |
final value |
|
||||
|
Trial |
Trial |
Trial |
Trial |
|||||
|
fv |
fv |
fv |
fv |
|||||
|
1 |
1,800 |
4 |
1,800 (1 + x)4 |
4,394.53 |
4,682.60 |
4,756.78 |
4,785.20 |
|
|
2 |
2,100 |
3 |
2,100 (1 + x)3 |
4,101.56 |
4,301.60 |
4,352.61 |
4,372.10 |
|
|
3 |
2,400 |
2 |
2,400 (1 + x)2 |
3,750 |
3,870.96 |
3,901.50 |
3,913.14 |
|
|
4 |
2,700 |
1 |
2,700 (1 + x)1 |
3,375 |
3,429 |
3,442.50 |
3,447.63 |
|
|
5 |
3,000 |
0 |
3,000 |
3,000 |
3,000 |
3,000 |
3,000 |
|
|
yields FV = Σ fv |
18,621.09 |
19,284.16 |
19,453.39 |
19,518.07 |
||||
|
O.K. |
||||||||
Trial No. 4 yields FV = Σ fv = £19,518.13 (£19,518.07 computed), and the Internal Rate of Return (IRR) received on our Net Outlays is therefore 27.69% p.a.
| Note! |
Using the parameters of this example, the logical equivalence of formulae (F7) and (F8) is proven as follows: |
FV = PV(1+i)n (Refer to the equation for the Final Value (FV)
in Example 5.1)
Here FV = PV(1+i)5 i.e. PV =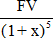
Therefore PV =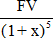
=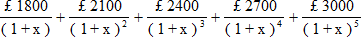
i.e PV= Σ pv
Having computed the Internal Rate of Return (IRR) @ 27.69% p.a., we can now compute the Equivalent Annual Cost of our investment by using the Uniform Series Formula (F4).
R=S 
S=£19,518.13
n=5 years
i=27.69% p.a.
givingR=£19,518.13 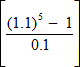
givingR=£2,257.01
Our Equivalent Annual Cost is therefore £2,257.01, with an Internal Rate of Return of 27.69% p.a.
It is obvious from the above Examples that the computation of the Internal Rate of Return is required first in order to calculate the Equivalent Annual Cost, except in the case where the Net end of year Outlays are already equal in value (as was the case in Example 5.5), in which case the Equivalent Annual Cost will be immediately obvious, i.e. equal to the Net end of year Outlay.
Example 5.7
Let us now compare the Net Outlays of Example 5.5 and Example 5.6 as two investment options (Investment Option A and Investment Option B) where the Final Values of our investments with the Building Society are equal, each yielding £19,518.13. A comparison of these Investment Options is represented on the following Comparison of Investment Options table.
|
Comparison of Investment Options |
||
|
Year |
Investment Option A Net Outlay |
Investment Option B Net Outlay |
|
1 |
£2,400 |
£1,800 |
|
2 |
£2,400 |
£2,100 |
|
3 |
£2,400 |
£2,400 |
|
4 |
£2,400 |
£2,700 |
|
5 |
£2,400 |
£3,000 |
|
Total Net Outlay |
£12,000 |
£12,000 |
|
Average Net Annual |
£2,400 |
£2,400 |
|
Final Value |
£19,518.13 |
£19,518.13 |
From the above Representation of the comparison of the investment options, one would be led to believe that the Investment Options presented in Example 5.5 and Example 5.6 are exactly equivalent, both Options ending in equal Final Values of £19,518.13 for an equal Average Net Annual Outlay of £2,400.
But we know from our Financial Analysis computations in Example 5.5 and Example 5.6 that SUCH IS NOT THE CASE.
The Internal Rate of Return (IRR) for Investment Option A (see Example 5.5) is 24.533% p.a., while that for Investment Option B (see Example 5.6) is 27.69% p.a. The Internal Rate of Return (IRR) comparison shows Investment Option B to be a better choice than Investment Option A; Option B provides us with a higher return on our investment.
It is equally evident that Investment Option B is a better choice than Investment Option A from a comparison of their Equivalent Annual Costs (again refer to Example 5.6 and Example 5.5, respectively). The Equivalent Annual Cost (EAC) of investing in Investment Option B is £2257.01 while that for Investment Option A is £2400.00.
So why, then, does the tabulated Representation, comparing Investment Option A and Investment Option B, show both Options with the same Average Net Annual Outlay?
The difference lies in the fact that £2,400 is merely the ARITHMETIC Average of the Net Annual Outlays and not the WEIGHTED Average.
The Arithmetic Average has NO MEANING WHATSOEVER in the context of Financial Analysis.
THE ‘ARITHMETIC AVERAGE’
TAKES NO ACCOUNT OF
THE ‘TIME VALUE OF MONEY’.
A government subsidy of £100 at the end of Year 1 is of much greater value than a government subsidy of £100 at the end of Year 4; the earlier we get the government subsidy the less it will cost us to yield our Final Value sum (FV), because the subsidy will have been gaining interest over a longer period of time. The Arithmetic Average takes no account of this fact.
For a true comparison between the Investment Options, each year’s Net Outlay must be weighted by its Time Value Weight Factor.
The Weighted Average Outlay is the Annual Outlay of the Annuity (i.e. Uniform Annual Series) whose Final Value exactly equals the Final Value of the investment.
Alternatively, the Weighted Average Outlay is the Annual Outlay of the Annuity whose Present Value exactly equals the Present Value of the investment.
The Weighted Average Outlay is therefore the Equivalent Annual Cost.
Let us now use the data of Example 5.5 and Example 5.6 to show this fact.
Investment Option A
|
|
Investment Process of Example 5.5 |
|
||||
|
|
IRR = 24.533% p.a. |
|
||||
|
Year |
Investment |
Investment |
Time : IRR Time Value Weight Factor (1 + x )n |
final value |
||
|
1 |
2,400 |
4 |
2.405126 |
5,772.30 |
||
|
2 |
2,400 |
3 |
1.931316 |
4,635.16 |
||
|
3 |
2,400 |
2 |
1.550847 |
3,722.03 |
||
|
4 |
2,400 |
1 |
1.24533 |
2,988.79 |
||
|
5 |
2,400 |
0 |
1 |
2,400.00 |
||
|
FV Required=£19,518.13 |
FV = Σ fv = |
19,518.28 |
||||
The Uniform Annual Series whose Final Value is £19,518.13, where the investment period is 5 years and the Internal Rate of Return is 24.533%, is given by Formula (F4).
R=S 
GivingR=£19,518.13 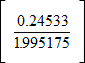
GivingR=£2,399.98 (i.e. £2,400.00)
Thus the Weighted Average Outlay in Example 5.5 is £2,400 per year i.e. the Equivalent Annual cost is £2,400 per year.
Note! The minor difference in the figures is due to end decimal rounding off.
The Weighted Average Outlay in this case is equal to the Arithmetic Average, ONLY because all of the yearly Net Outlays are already EQUAL in amount, –– i.e. they are ALREADY in the form of a Uniform Annual Series.
–––––– REMEMBER THIS !
Note! We already know this from the computations of Example 5.5; this presentation is to clarify the Investment Process and to highlight the comparison with the data of Example 5.6 that follows.
Investment Option B
|
|
Investment Process of Example 5.6 |
|
||||
|
|
IRR = 27.69% p.a. |
|
||||
|
Year |
Investment |
Investment |
Time : IRR |
final value |
||
|
1 |
1,800 |
4 |
2.658444 |
4,785.20 |
||
|
2 |
2,100 |
3 |
2.081952 |
4,372.10 |
||
|
3 |
2,400 |
2 |
1.630474 |
3,913.14 |
||
|
4 |
2,700 |
1 |
1.2769 |
3,447.63 |
||
|
5 |
3,000 |
0 |
1 |
3,000.00 |
||
|
FV Required=£19,518.13 |
FV = Σ fv = |
19,518.07 |
||||
The Uniform Annual Series whose Final Value is £19,518.13, where the investment period is 5 years and the Internal Rate of Return is 27.69%, is given by Formula (F4).
R=S 
GivingR=£19,518.13 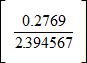
GivingR=£2,257.01
Thus the Weighted Average Outlay in Example 5.6 is £2,257.01 per year,
i.e. the Equivalent Annual Cost is £2257.01.
From the above Examples, it must be clear that, in order to make an informed decision between two Investment Options, we must be able to make a truthful comparison between their Financial Analysis parameters; we must be able to compare their Internal Rate of Return (IRR) or their Equivalent Annual Cost (EAC).
It must also be clear that the investment comparison as represented in the Comparison of Investment Options table in Example 5.7 is not a truthful comparison. ———— It gives a false impression.
You will recall from Example 5.6 that the Internal Rate of Return (IRR) on our investment was computed by:
| (a) |
using Trial Values (x%) of the Internal Rate of Return (IRR) to compute the final value (fv) of each year's Net Outlay, Summating these final values (Σfv), and comparing this Summation (Σfv) to the actual Final Value (FV) yielded by the investment, and |
| (b) |
repetition of this process until the Trial Value (x%) of the Internal Rate of Return (IRR) was such that the resultant Σ fv equated to the actual Final Value (FV) of £19,518.13 yielded by the investment. |
The computation format of Example 5.6 was used to show how the analysis of the investment process worked, and the ‘Summation of final values’ ( Σ fv) iterative process employed is the clearest method of analysis, in that it tracks each year’s Net Outlay directly to final value.
However, you will recall from Formula (F8) (see Example 5.6)
thatPV = Σ pv
andFV=PV (1+x)n
ThereforeFV=(Σ pv ) (1+x)n
---------------
Where there is a considerable number of investment periods involved, final value (fv) figures become cumbersome when being computed manually. It is sometimes more convenient to compute the Internal Rate of Return (IRR) on our investment by employing an iterative process using the ‘Summation of present values’ (Σpv) and, from this Summation, computing a Final Value (FV) for comparison with the actual Final Value yielded by the investment.
This process is logically equivalent to the ‘Summation of final values’ (Σfv) iterative process employed above.
NOTE!
The mathematical process of 'Iteration' is most easily done by computer, where a simple 'do-loop' or 'for-loop' can repeat a mathematical process ad infinitum until the solution is achieved. Any Financial Institution could execute the processes of Iteration necessary to the various Financial Analyses, as set out in this website-book, at the push of a button.
But, as stated at the outset of this Chapter, we are setting out to provide ABSOLUTE PROOF —— on a 'first principles' basis.
---------------
With the ‘Summation of present values’ (Σ pv) iterative process, the Internal Rate of Return (IRR) is computed by:
| (a) |
using Trial Values (x%) of the Internal Rate of Return to compute the present value (pv) of each year's Net Outlay, Summating these present values (Σ pv), then computing the Final Value (FV) using this Summation (Σ pv) and the Trial Value (x%) of the Internal Rate of Return, and then comparing this computed Final Value (FV) to the actual Final Value yielded by the investment, and |
| (b) |
repetition of this process until the Trial Value (x%) of the Internal Rate of Return (IRR) is such that the resulting computed Final Value (FV) equates to the actual Final Value yielded by the investment. |
Note! It is this ‘Summation of present values’ (Σ pv) process of Iteration that we will use in Chapter 8 and Chapter 9 to carry out our Financial Analysis of the Case 1 and Case 2 Mortgage Quotations, and, thereby, to expose how the Financial Institutions have distorted the truth.
We will now illustrate the ‘Summation of present values’ (Σ pv) process of Iteration, by example. We will use the same data as was used previously in Example 5.6, where the ‘Summation of final values’ (Σ fv) process of Iteration was used. Cross-comparison with the computation format used in Example 5.6 will further clarify the equivalence of both methods.
Example 5.8
Our Gross Annual Cost of investment in a Building Society is £3,000 per year at the end of each year for a period of 5 years, and this choice of investment means that we will receive a government subsidy at the end of each of the five years. This government subsidy will vary linearly over the five years as follows:
ForYear 1Subsidy=40% of Gross Investment
ForYear 2Subsidy=30% of Gross Investment
ForYear 3Subsidy=20% of Gross Investment
ForYear 4Subsidy=10% of Gross Investment
ForYear 5Subsidy=0% of Gross Investment
If the investment interest rate paid by the Building Society on our investment is 13.2% p.a., our investment thereby yielding a Final Value of £19,518.13 from the Building Society, what Internal Rate of Return (IRR) have we achieved on our Net Outlays and what was our Equivalent Annual Cost (EAC) for this investment ?
We first compute the Net Outlay for each year by tabulating as follows:
|
Year |
Gross Outlay |
Government |
Net Outlay |
|
1 |
£3,000 |
£1,200 |
£1,800 |
|
2 |
£3,000 |
£900 |
£2,100 |
|
3 |
£3,000 |
£600 |
£2,400 |
|
4 |
£3,000 |
£300 |
£2,700 |
|
5 |
£3,000 |
Zero |
£3,000 |
Let the Internal Rate of Return (IRR) = x% p.a.
The Present Value (PV) of our investment, this being the Time Zero value of the Final Value (FV) of our investment discounted at the Internal Rate of Return of x% p.a., IS EQUAL TO the Sum of the present values (Σ pv) of each year's Net Outlay, these being the Time Zero values of each year's Net Outlay discounted at the Internal Rate of Return of x% p.a.
In Example 5.8 our Final Value is £19,518.13.
We want to compute the value of the Internal Rate of Return, x% p.a., such that: when we invest Σpv, the Sum of the present values of each year's Net Outlay (the present value of each year's Net Outlay being computed by discounting that year's Net Outlay to Time Zero by x% p.a.), at x% p.a. over 5 years, this will yield a Final Value of £19,518.13.
PV=Σ pv
Remember!P=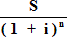
The present value (pv) of the end of the first year’s Net Outlay of £1800 is
therefore pv = 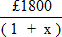 , Time Zero being at the beginning of the first year.
, Time Zero being at the beginning of the first year.
Σ pv is calculated by tabulating each year's present value (pv) as follows:
|
Year |
Net Outlay |
|
|
1 |
1,800 |
1800 |
|
2 |
2,100 |
2100 |
|
3 |
2,400 |
2400 |
|
4 |
2,700 |
2700 |
|
5 |
3,000 |
3000 |
Σ pv=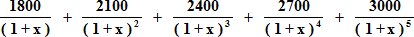
FV=(Σ pv) (1+x)5=£19,518.13
The value of the Internal Rate of Return, x% p.a., that makes this expression [i.e. the above equation for the Final Value (FV)] valid is computed using Iteration. This ‘trial and error’ process is most clearly done by tabulation, as follows:
|
Year |
Net Outlay |
present value |
|
||||
|
Trial No. 1 |
Trial No. 2 |
Trial No. 3 |
Trial No. 4 |
||||
|
pv |
pv |
pv |
pv |
||||
|
1 |
1,800 |
1800 |
1,440 |
1,417.32 |
1,411.76 |
1,409.66 |
|
|
2 |
2,100 |
2100 |
1,344 |
1,302 |
1,291.81 |
1,287.97 |
|
|
3 |
2,400 |
2400 |
1,228.80 |
1,171.66 |
1,157.93 |
1,152.76 |
|
|
4 |
2,700 |
2700 |
1,105.92 |
1,037.88 |
1,021.70 |
1,015.63 |
|
|
5 |
3,000 |
3000 |
983.04 |
908.04 |
890.37 |
883.77 |
|
|
Σ pv |
6,101.76 |
5,836.90 |
5,773.57 |
5,749.79 |
|||
|
yields FV |
18,621.09 |
19,284.17 |
19,453.39 |
19,518.05 |
|||
|
Remember!FV = (Σ pv) (1+x)5 |
O.K. |
||||||
Trial No. 4 yields FV = £5,749.79 (1.2769)5 = £19,518.13 (£19,518.05 computed), and the Internal Rate of Return (IRR) achieved on our Net Outlays is therefore 27.69% p.a.
Hence, the Equivalent Annual Cost (as already computed in Example 5.6), using the Uniform Series Formula (F4), is £2,257.01.
Note! Compare the above tabulation to that in Example 5.6 and you will see that both methods of analysis are logically equivalent.
We now have some understanding of the Basic Tools of Investment Analysis. We know that in order to make an informed decision between two Investment Options we must be able to compare their Internal Rate of Return or their Equivalent Annual Cost.
But, unfortunately, it’s not that simple!
Some Investment Options carry more Risk than others.
In order to make a fully informed decision between two Investment Options, we also need to know the measure of the financial Risk associated with each Investment Option. And, if one Investment Option carries a higher Risk than the other, but also offers a higher Internal Rate of Return, we need to know if this expected Excess Return (i.e. Reward) justifies taking the higher Risk. These critical Financial Analysis parameters, i.e. Risk, and Reward for Risk taken, we will discuss in Chapter 7.
But first, we will use the knowledge we have acquired thus far to assess the manner in which Mortgage Interest is charged, and to highlight the financially injurious consequences for the borrower / investor where the Financial Institution does not comply with the necessary (and legal) disclosure requirements for indicating the true Cost of Credit.